问题
解答题
设M为部分正整数组成的集合,数列{an}的首项a1=1,前n项和为Sn,已知对任意整数k属于M,当n>k时,Sn+k+Sn-k=2(Sn+Sk)都成立。
(1)设M={1},a2=2,求a5的值;
(2)设M={3,4},求数列{an}的通项公式。
答案
解:(1)∵k=1,
∴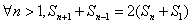 ,
,
∴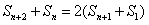 ,
,
即: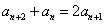 ,
,
所以,n>1时,{an}成等差,而a2=2,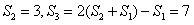 ,
,
∴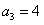 ,∴
,∴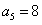 。
。
(2)由题意: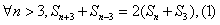 ,
,
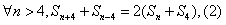 ,
,
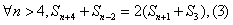 ,
,
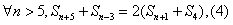 ,
,
当n≥5时,由(1)(2)得: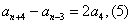 ,
,
由(3)(4)得: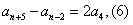 ,
,
由(1)(3)得: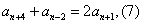 ,
,
由(2)(4)得: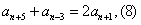 ,
,
由(7)(8)知: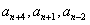 成等差,
成等差,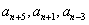 成等差;
成等差;
设公差分别为:d1,d2,
由(5)(6)得: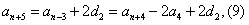 ,
,
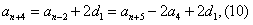 ,
,
由(9)(10)得: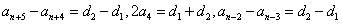 ,
,
∴{an}(n≥2)成等差,设公差为d,
在(1)(2)中分别取n=4,n=5得:
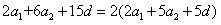 ,即
,即 ,
,
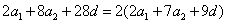 ,即
,即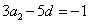 ,
,
∴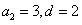 ,∴
,∴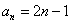 。
。
