∵a_n+3=a_n，∴数列{a_n}为周期为3的周期数列，∴a₂₀₁₀=a_3×670=a3=

2

3

，a₂₀₀₉=a2=

3

2

，a₂₀₁₁=a1=

1

3

∴f（a₂₀₁₁）=f（

1

3

），f（a₂₀₀₉）=f（

3

2

）=f（2-

1

2

）=f（

1

2

），f（a₂₀₁₀）=f（

2

3

）

∵f（x）=f（2-x），∴函数f（x）的图象关于x=1对称，又∵当x≤1时，f（x）=|1-a^x|（a＞1），故函数f（x）的图象如图：

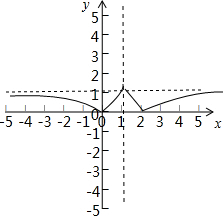
函数f（x）在（0，1）上为增函数，

∵

1

3

＜

1

2

＜

2

3

，∴f（

1

3

）＜f（

1

2

）＜f（

2

3

）

即f（a₂₀₁₁）＜f（a₂₀₀₉）＜f（a₂₀₁₀）

故选 B