问题
填空题
已知函数f(x)=
|
答案
∵a-x≥0,x≥0,∴0≤x≤a,∴定义域为[0,a]
对定义域内任意x1,x2,满足|f(x1)-f(x2)|<1,即表明f(x)的最大值与最小值的差小于1.(也就是值域区间的长度小于1),求其最大最小值即可
∵f(x)=
+a-x
≥0x
∴[f(x)]2=a+2
≥a,当x=0或a时,f(x)取最小值x(a-x) a
又x(a-x)≤[
]2=x+(a-x) 2
,当x=a-x即x=a2 4
时取等号a 2
即[f(x)]2≤a+a=2a,f(x)≤
,当x=2a
时取最大值a 2 2a
∴(
-1)2
<1a
∴
<a
=1+1
-12 2
∴a<3+22
∵a∈N*,
∴a=1、2、3、4、5
∴正整数a的取值个数是5个.
故答案为:5

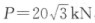 ,方向如图示。支座A的反力沿水平和铅直方向的分力XA、YA的大小分别为()。
,方向如图示。支座A的反力沿水平和铅直方向的分力XA、YA的大小分别为()。