问题
解答题
已知等比数列{an}的前n项和为Sn，若am，am+2，am+1（m∈N*）成等差数列，试判断Sm，Sm+2，Sm+1 是否成等差数列，并证明你的结论。
答案
解：设等比数列{an}的首项为a1，公比为q（a1≠0，q≠0），
若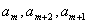
成等差数列，
则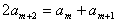
∴
∵
∴
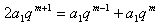
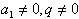
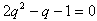
解得q=1或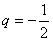
当q=1时，∵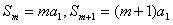
，
∴
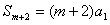
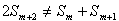
∴①当q=1时，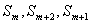
不成等差数列
②当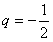
时，
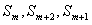成等差数列，下面给出它的证明方法
∵
∴
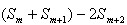
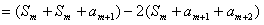
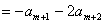
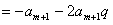
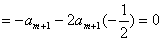
∴当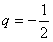
时，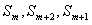
成等差数列。