问题
问答题
已知函数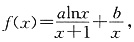 曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.
曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.
(1)求a、b的值;
(2)如果当x>0,且x≠1时,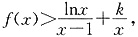 求k的取值范围.
求k的取值范围.
答案
参考答案:
(1)
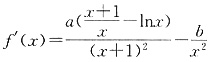
由于直线x+2y-3=0的斜率为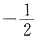 ,且过点(1,1),故
,且过点(1,1),故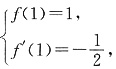 即
即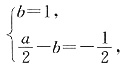 解得a=1,b=1.
解得a=1,b=1.
(2)由(1)知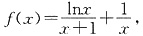 所以
所以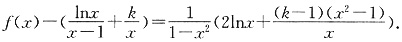
考虑函数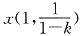 ,则
,则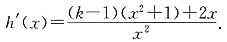
①设k≤0,由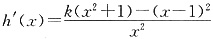 知,当x≠1时,h′(x)<0.而h(1)=0,故
知,当x≠1时,h′(x)<0.而h(1)=0,故
当x∈(0,1)时,h(x)>0,可得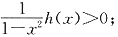
当x∈(1,+∞)时,h(x)<0,可得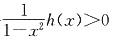
从而当x>0,且x≠1时,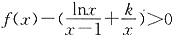 ,即
,即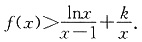
②设0<k<1.由于当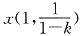 时,(k-1)(x2+1)+2x>0,故h′(x)>0,而h(1)=0,
时,(k-1)(x2+1)+2x>0,故h′(x)>0,而h(1)=0,
故当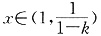 时,h(x)>0,可得
时,h(x)>0,可得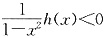 ,与题设矛盾,
,与题设矛盾,
③设k≥1,此时h′(x)>0,而h(1)=0,故当x∈(1,+∞)时,h(x)>0,可得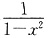 h(x)<0,与题设矛盾,
h(x)<0,与题设矛盾,
综合得,k的取值范围为(-∞,0].
