问题
证明题
已知Sn是等比数列｛an｝的前n项和，S3，S9，S6成等差数列，求证：a2，a8，a5成等差数列。
答案
证明：因为S3，S9，S6成等差数列，所以公比q≠1，且2S9=S3+S6
即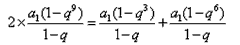
，
于是2q9=q3+q6，即2q6=1+q3
上式两边同乘以a1q，得2a1q7=a1q+a1q4
即2a8=a2+a5
所以a2，a8，a5成等差数列。
搜题请搜索小程序“爱下问搜题”
已知Sn是等比数列｛an｝的前n项和，S3，S9，S6成等差数列，求证：a2，a8，a5成等差数列。
证明：因为S3，S9，S6成等差数列，所以公比q≠1，且2S9=S3+S6
即，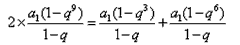
于是2q9=q3+q6，即2q6=1+q3
上式两边同乘以a1q，得2a1q7=a1q+a1q4
即2a8=a2+a5
所以a2，a8，a5成等差数列。