甲、乙、丙三人同时独立地向同一目标射击,各打一发子弹,命中率分别为0.4,0.5和0.6,目标中一、二、三弹而被击毁的概率分别为0.2,0.4和0.8.
(Ⅰ) 求目标被击毁的概率P;
(Ⅱ) 已知目标被击毁,求目标中三弹的概率q.
参考答案:设A表示事件“目标被击毁”,Bi表示事件“目标中i弹”(i=0,1,2,3),由事件的独立性,得
P(B0)=(1-0.4)(1-0.5)(1-0.6)=0.12,
P(B1)=0.4×(1-0.5)(1-0.6)+(1-0.4)×0.5×(1-0.6)+(1-0.4)(1-0.5)×0.6
=0.38,
P(B2)=0.4×0.5×(1-0.6)+0.4×(1-0.5)×0.6+(1-0.4)×0.5×0.6=0.38,
P(B3)=0.4×0.5×0.6=0.12.
事件B0,B1,B2和B3是该随机试验的完备事件组.
(Ⅰ)根据全概率公式,得
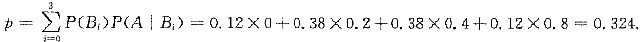
(Ⅱ)根据贝叶斯公式,得

解析:
[分析]: 目标中一弹有三种情形:甲击中目标而乙和丙未击中;乙击中目标而甲和丙未击中;丙击中目标而甲和乙未击中.目标中二弹也有三种情形,而目标中三弹只有一种情形.没有一弹击中目标也只有一种情形,且此时目标肯定没有被击毁.利用独立性可求得目标中i(i=0,1,2,3)弹的概率,利用全概率公式可求得p,利用贝叶斯公式可求得q.