问题
问答题
设u=z(x2+3),求向量场A=gradu通过上半球面S:x2+y2+z2=1(z>0)的上侧的流量.
答案
参考答案:由u=z(x2+3),有
A=gradu={2xz,0,x2+3},
则流量
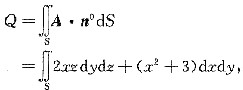
其中S为球面x2+y2+z2=1(z>0)的上侧.添一块
S1={(x,y,z)|x2+y2≤1,z=0),
指向z轴负向,S1在xOy平面上的投影域为D1,S1与S围成的闭区域记为Ω,因此有
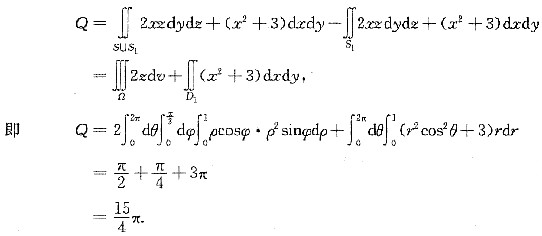
解析:
[分析]: 根据题设,先将流量写成曲面积分表达式,按第二型曲面积分计算,添补一块面,使积分域为封闭曲面,以便利用高斯公式算出结果.
