问题
问答题
设总体X的概率密度为
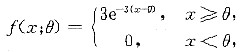
其中θ是未知参数．
(Ⅰ) 求θ的矩估计量，判断它是否为θ的无偏估计量；
(Ⅱ) 求θ的最大似然估计量，判断它是否为θ的无偏估计量．
答案
参考答案：设X1，X2，…，Xn是来自总体X的样本，x1，x2，…，xn是样本值，
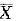是样本均值．
(Ⅰ)由于
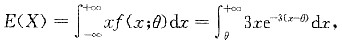
令t=x-θ，得
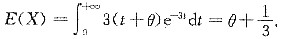
得θ的矩估计量为
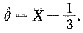
因为
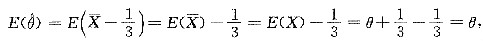
所以
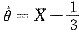是θ的无偏估计量．
(Ⅱ)似然函数为
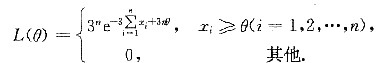
当xi≥θ(i=1，2，…，n)时，L(θ)＞0，且θ越大，L(θ)越大，取
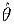=min(x1，x2，…，xn)，有L(
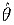)≥L(θ)．θ的最大似然估计量为
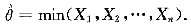
X的分布函数为
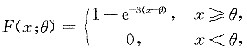
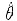=min(X1，X2，…，Xn)的分布函数为
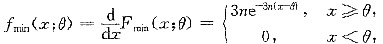
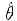的概率密度为
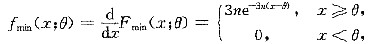
由此可得
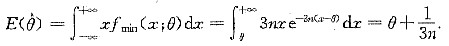
因为
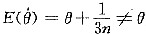，所以
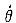=min(X1，X2，…，Xn)不是θ的无偏估计量．
解析：
[分析]： 容易求解(Ⅰ)．根据似然函数表达式寻找其最大值点，作为θ的最大似然估计．求出该估计量的分布函数，进而求得其概率密度及数学期望，判断其是否为θ的无偏估计量．