∵f（x）是定义在R上的偶函数，当0≤x≤1时，f（x）=x²，

∴当-1≤x≤0时，0≤-x≤1，f（-x）=（-x）²=x²=f（x），

又f（x+2）=f（x），

∴f（x）是周期为2的函数，又直线y=x+a与函数y=f（x）的图象在[0，2]内恰有两个不同的公共点，其图象如下：

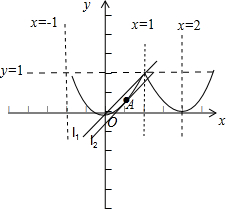
当a=0时，直线y=x+a变为直线l₁，其方程为：y=x，显然，l₁与函数y=f（x）的图象在[0，2]内恰有两个不同的公共点；

当a≠0时，直线y=x+a与函数y=f（x）的图象在[0，2]内恰有两个不同的公共点，由图可知，直线y=x+a与函数y=f（x）相切，切点的横坐标x₀∈[0，1]．

由

y=x+a y=x2

得：x²-x-a=0，由△=1+4a=0得a=-

1

4

，此时，x₀=x=

1

2

∈[0，1]．

综上所述，a=-

1

4

或a=0．

故答案为：-

1

4

或a=0．