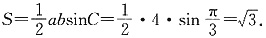问题
问答题
已知△ABC的角A、B、C所对的边分别是a、b、c，设向量
p=(b-2，a-2).
(1)若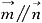
，求证：△ABC为等腰三角形；
(2)若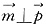
，边长C=2，角
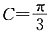，求△ABC的面积．
答案
参考答案：
(1)证明：∵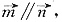
∴asinA=bsinB，
即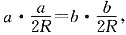
其中R是三角形ABC外接圆半径，
∴a=b.
∴△ABC为等腰三角形．
(2)解：由题意可知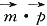
=0，即a(b-2)+b(a-2)一0．
∴a+b=ab.
由余弦定理可知，4=a2+b2-ab=(a+b)2-3ab
即(ab)2-3ab-4=0.
∴ab=4(舍去ab=-1)，
∴