问题
问答题
已知函数f（x）=x3+ax2+3bx+c（b≠0），且g（x）=f（x）-2是奇函数。
（1）求a，c的值；
（2）求函数，f（x）的单调区间。
答案
参考答案：
∵函数g(x)=f(x)-2为奇函数，
∴对任意的x∈R，g(-x)=-g(x)，即f(-x)-2=-f(x)+2。
又f(x)=x3+ax2+3bx+c，
∴-x3+ax2-3bx+c-2=-x3-ax2-3bx-c+2，
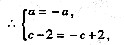
解得a=0，c=2。
(2)由(1)得f(x)=x3+3bx+2，
故f’(x)=3x2+3b(b≠0)。
当b＜0时，由f’(x)=0得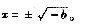
f’(x)随x的变化而变化的情况，如下表。
所以当b＜0时，函数f(x)在区间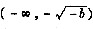
上单调递增，
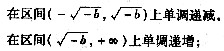
当b＞O时f’(x)＞0，函数f(x)在(-∞，+∞)上单调递增。