问题
问答题
设函数f(x)有界，且f’(x)连续，x∈(-∞，+∞)，又
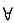x∈(-∞，+∞)，有|f(x)+f’(x)|≤1，试证：|f(x)|≤1．
答案
参考答案：作辅助函数F(x)=exf(x)，则
[*]
即 |f(x)|≤1．
解析：
[分析]： 采用构造辅助函数法，由欲证结论
[*]
试想把exf(x)取作辅助函数F(x)，则其导函数F’(x)=ex[f(x)+f’(x)]，显然，由题设可以估计F’(x)了，再往下积分即可．