问题
问答题
化二次型
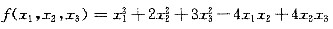为规范型，并写出所做的可逆线性变换．
答案
参考答案：解法一
配方法：[*]
令y1=x1-2x2，[*]得到规范型
[*]
对应变换为[*]
解法二 正交变换：二次型对应系数矩阵[*]由于
[*]
所以特征值为λ1=5，λ2=2，λ3=-1．
λ1=5对应特征向量[*]单位化得[*]
λ2=2对应特征向量[*]单位化得[*]
λ3=-1对应特征向量[*]单位化得[*]
令[*]则[*]
作变换[*]则有[*]
再作变换[*]即[*]则得到规范型
[*]
所作的变换为X=PZ=PDY=CY，
这里，[*]
解析：
[分析]： 这是一常规题．解法常用配方法和正交变换．