问题
问答题
设
 证明:
证明:
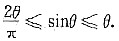
答案
参考答案:令[*]
[*]
因为θ-tanθ<0,[*]
故f(θ)单调减,[*]
当θ>0时,有f(θ)<f(0)=1;
当[*]
因此有[*]
即[*]
解析:
[分析]: 当θ=0时,不等式显然成立.
当[*]欲证[*]可令[*]定义f(0)=1,利用f(θ)的单调性,[*]
即可证得.
设
 证明:
证明:
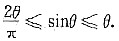
参考答案:令[*]
[*]
因为θ-tanθ<0,[*]
故f(θ)单调减,[*]
当θ>0时,有f(θ)<f(0)=1;
当[*]
因此有[*]
即[*]
解析:
[分析]: 当θ=0时,不等式显然成立.
当[*]欲证[*]可令[*]定义f(0)=1,利用f(θ)的单调性,[*]
即可证得.