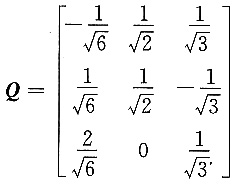问题
问答题
设二次型
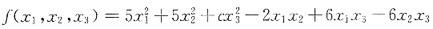 所对应的矩阵为A,且方程组Ax=0有非零解,
所对应的矩阵为A,且方程组Ax=0有非零解,
将二次型化为标准型,并写出正交变换矩阵.
答案
参考答案:
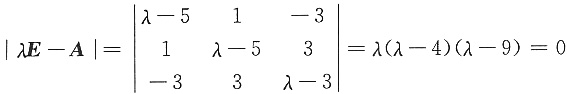 则特征值为0,4,9.
则特征值为0,4,9.
将特征值分别代入(λE-A)x=0,可求得
λ=0对应的特征向量为:
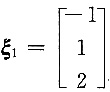 ,单位化为
,单位化为

λ=4对应的特征向量为:
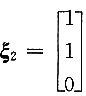 ,单位化为
,单位化为

λ=9对应的特征向量为:
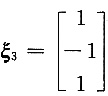 ,单位化为
,单位化为
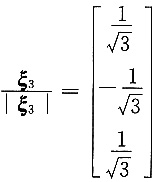
故二次型的标准形为
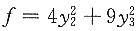 ,所作正交变换矩阵为
,所作正交变换矩阵为
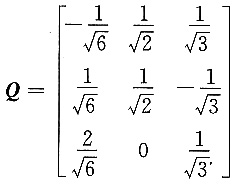
设二次型
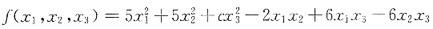 所对应的矩阵为A,且方程组Ax=0有非零解,
所对应的矩阵为A,且方程组Ax=0有非零解,
将二次型化为标准型,并写出正交变换矩阵.
参考答案:
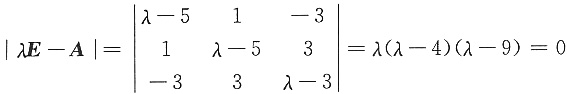 则特征值为0,4,9.
则特征值为0,4,9.
将特征值分别代入(λE-A)x=0,可求得
λ=0对应的特征向量为:
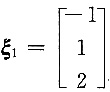 ,单位化为
,单位化为

λ=4对应的特征向量为:
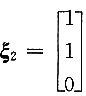 ,单位化为
,单位化为

λ=9对应的特征向量为:
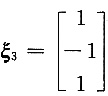 ,单位化为
,单位化为

故二次型的标准形为
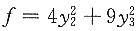 ,所作正交变换矩阵为
,所作正交变换矩阵为