问题
单项选择题
设α1，α2，…，αs是Rn上一组线性相关的向量，但α1，α2，…，αs中任意s-1个向量都线性无关，若存在常数k1，k2，…，ks，使得
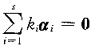，则ki
A．全为0．
B．全不为0．
C．或者全为0，或者全不为0．
D．不能确定．
答案
参考答案：C
解析：[详解] 显然，ki全为零，可使
．
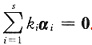又因为α1，α2，…，αs线性相关，则存在一组不全为零的数ki(i=1，2，…，s)，使得
．
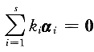下列ki全不为零．若ki中有为零的数，不妨设k1=0，则
，而ki(i=2，…，s)不全为零，所以α2，α3，…，αs线性相关，与题设矛盾．
所以ki全不为零．故选(C)．