问题
问答题
设
 在第一象限内具有连续的二阶导数,
在第一象限内具有连续的二阶导数,
 ,且
,且
 ,求f(x)在区间[1,2]上的平均值.
,求f(x)在区间[1,2]上的平均值.
答案
参考答案:先求出f(x)的表达式,然后求其在[1,2]上的平均值.
令
 ,则
,则
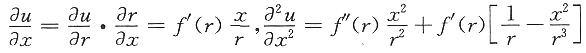 ,
,
同理,
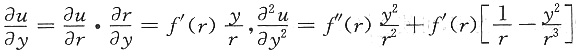 .
.
将
 代入
代入
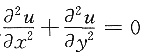 中可得
中可得
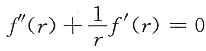 ,则[rf’(r)]’=0,积分可得
,则[rf’(r)]’=0,积分可得
f(r)=C1lnr+C2.
又由条件
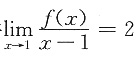 知f(1)=0,f’(1)=2,代入f(r)=C1lnr+C2可得
知f(1)=0,f’(1)=2,代入f(r)=C1lnr+C2可得
C1=2,C2=0.
故f(r)=2lnr,即f(x)=2lnx.故f(x)在区间[1,2]上的平均值为
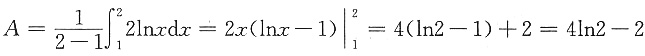 .
.




