问题
问答题
设α1，α2，β1，β2均是三维列向量，且α1，α2线性无关，β1，β2线性无关，证明存在非零向量ξ，使得ξ既可由α1，α2线性表出，又可由β1，β2线性表出；
答案
参考答案：四个三维向量α1，α2，β1，β2必线性相关，故存在不全为零的常数k1，k2，λ1，λ2，使得
k1α1+k2α2+λ1β1+λ2β2=0，
即k1α1+k2α2=-λ1β1-λ2β2．
其中k1，k2不全为零(否则，由
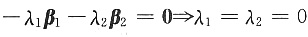，这和k1，k2，λ1，λ2不全为零相矛盾)．
令ξ=k1α1+k2α2=-λ1β1-λ2β2≠0，则ξ即为所求．
