问题
问答题
已知向量组

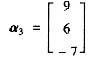 有相同的秩,且β3可由α1,α2,α3线性表出,求a,b的值.
有相同的秩,且β3可由α1,α2,α3线性表出,求a,b的值.
答案
参考答案:解法一 因为α1,α2线性无关,而α3=3α1+2α2,所以秩r(α1,α2,α3)=2.因此r(β1,β2,β3)=2.从而
[*]
又因β3可以由α1,α2,α3线性表出,那么β3必可用极大线性无关组α1,α2线性表出.于是方程组x1α1+x2α2=β3有解.由
[*]
解法二 因为β3可由α1,α2,α3线性表出,故方程组x1α1+x2α2+x3α3=β3有解.
[*]
解析:本题有两个信息,相同的秩以及卢β3可以由α1,α2,α3线性表出.由于α1,α2,α3的坐标是己知的,故可由秩r(α1,α2,α3)入手,转化为r(β1,β2,β3),从而可得到a与b所满足的关系式,然后再用第二个信息确定a与b的取值.当然也可先从x1α1+x2α2+x3α3=β3有解,求出b,然后再用第一个信息求a.
