问题
问答题
欲用围墙围成面积216m2的一块矩形土地，并在中间用一堵墙将其隔成两块，问这块土地的长和宽选取多大的尺寸，才能使建造围墙所用材料最省？
答案
参考答案：
设围墙的总长为S(总长最短，用料最省)，土地长为x，宽为y，由题意应有关系式 S=2x+3y．
由于面积216=xy，所以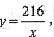
从而围墙总长S与土地的长x的函数关系为
因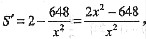
令S’=0，得x=18；又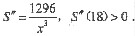
所以x=18是函数的极小值点，依题意，也是最小值点，这时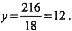
答：当这块土地长为18m、宽为12m时，建造围墙所用材料最省．