问题
填空题
曲线f（x）=xlnx-x在x=e处的法线方程为（）.
答案
参考答案：y+x-e=0
解析：
因为 f(e)=elne-e=0，
f’(x)=lnx+1-1=lnx，f’(e)=lne=1，
所以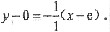
故所求法线方程为y+x-e=0．
搜题请搜索小程序“爱下问搜题”
曲线f（x）=xlnx-x在x=e处的法线方程为（）.
参考答案：y+x-e=0
解析：
因为 f(e)=elne-e=0，
f’(x)=lnx+1-1=lnx，f’(e)=lne=1，
所以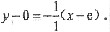
故所求法线方程为y+x-e=0．