已知
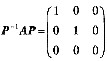 ,Aα1=α1,Aα2=α2,Aα3=0,其α1,α2,α3均为3维非零列向量,且α1,α2线性无关,则矩形P不能为( ).
,Aα1=α1,Aα2=α2,Aα3=0,其α1,α2,α3均为3维非零列向量,且α1,α2线性无关,则矩形P不能为( ).
参考答案:D
解析:将可逆矩阵P按列向量分块记为P=(ξ1 ξ2 ξ3),则
[*]
[*](Aξ1 Aξ2 Aξ3)=(ξ1 ξ2 0)
[*]Aξ1=ξ1,Aξ2=ξ2,Aξ3=0,
则ξ1,ξ2为A的属于特征值1的线性无关的特征向量,ξ3为A的属于特征值0的特征向量.
由题设知α1,α2是A的属于特征值1的线性无关的特征向量,α3是A的属于特征值0的特征向量,所以P=(α2 α1 α3)是合适的,所以排除(B).
据特征值的性质:“若ξ是A的属于特征值λ的线性无关的特征向量,k≠0,则kξ也是A的属于特征值λ的线性无关的特征向量”,可推得P=(-α1 5α2 α3)是合适的,所以排除(A).
据特征值的性质:“若ξ,η均为A的属于λ的线性无关的特征向量,k,t为不全为零的数,则kξ+tη也是A的属于λ的特征向量,”可推得α1+α2也是A的属于1的特征向量,注意到当α1,α2线性无关时,α1+α2,α2也相性无关,所以P=(α1+α2 α2 α3)是合适的,据此排除(C).
据特征值的性质:“若ξ,η是A的属于不同特征值的特征向量,则ξ+η不是A的特征向量”知α2+α3不是A的特征向量,故P不能为(α1 α2 α2+α3),所以应填(D).
