问题
问答题
证明级数
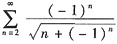条件收敛．
答案
参考答案：[证明]
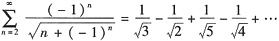是交错级数，但不满足莱布尼茨判别法的条件，而
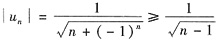，所以由比较判别法知，
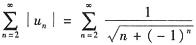发散．
又因为
．
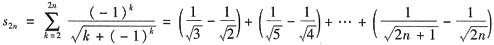由于上式每个括号都小于0，所以{s2n}单调递减，且由
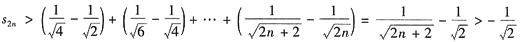，即{s2n}单调递减有下界，故{s2n}收敛，记
，易知
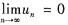，则
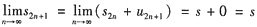，即{s2n+1}收敛．
综上，级数
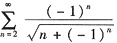条件收敛．
搜题请搜索小程序“爱下问搜题”
证明级数
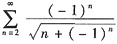条件收敛．
参考答案：[证明]
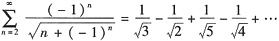是交错级数，但不满足莱布尼茨判别法的条件，而
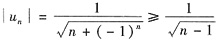，所以由比较判别法知，
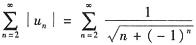发散．
又因为
．
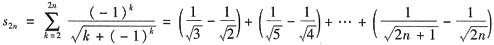由于上式每个括号都小于0，所以{s2n}单调递减，且由
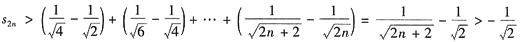，即{s2n}单调递减有下界，故{s2n}收敛，记
，易知
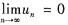，则
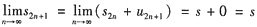，即{s2n+1}收敛．
综上，级数
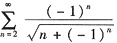条件收敛．
