问题
问答题
设函数f(u)具有二阶连续导数,而z=f(exsiny)满足
 ,求f(u).
,求f(u).
答案
参考答案:由复合函数求导法则,
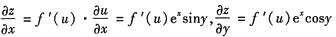 .
.
故
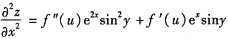 ,
,
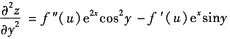 .
.
代入原方程,得
f"(u)e2x=e2xf(u),(z=f(u)),
即有f"(u)-f(u)=0,其特征方程为λ2-1=0,特征根为λ1,2=±1,因此其通解为f(u)=C1ex+C2e-x,其中C1,C2为任意常数.
设函数f(u)具有二阶连续导数,而z=f(exsiny)满足
 ,求f(u).
,求f(u).
参考答案:由复合函数求导法则,
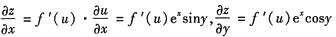 .
.
故
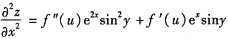 ,
,
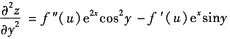 .
.
代入原方程,得
f"(u)e2x=e2xf(u),(z=f(u)),
即有f"(u)-f(u)=0,其特征方程为λ2-1=0,特征根为λ1,2=±1,因此其通解为f(u)=C1ex+C2e-x,其中C1,C2为任意常数.