问题
问答题
设y=y(x)是一向上凸的连续曲线，其上任意一点(x，y)处的曲率为
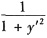，且此曲线上点(0，1)处的切线方程为y=x+1，求该曲线方程．
答案
参考答案：因曲线上凸，故有y"＜0．由曲率计算公式，得
，
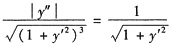即y"=-(1+y’2)，这是不显含x也不显含y的可降价方程．令p=y’，则y"=p’，上述微分方程可化为
p’=-(1+p2)，
解此可分离变量的微分方程可得arctanp=C1-x，即arctany’=C1-x．
由曲线过点(0，1)，且在该点切线方程为y=x+1，可得初始条件y(0)=1，y’(0)=1．故由y’(0)=1，得
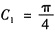，因此
，
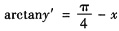即
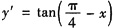，等式两端积分可得
．
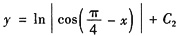由y(0)=1，得
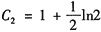．因此所求曲线方程为
．
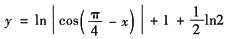