问题
问答题
求解二阶微分方程满足初始条件的特解
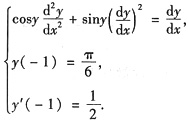
答案
参考答案：令
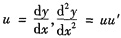，则原方程化为ucosy·u’+u2siny=u．当u=0，y=c不符合初始条件，舍去．
当u≠0时，得到
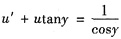，解为
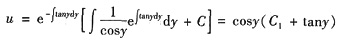
y’=cosy(C1+tany)，
由y(-1)=
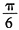，y’(-1)=
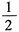，得C1=0．因此y’=siny．
解方程
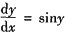得ln|cscy-coty|=x+C2，由
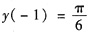得
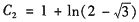，则所求微分方程满足初始条件的解为
．
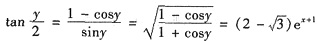所以y=
．