问题
问答题
设函数y=y(x)在(-∞，+∞)内具有二阶导数，且y’≠0，x=x(y)是y=y(x)的反函数．
试将x=x(y)所满足的微分方程[*]变换为y=y(x)满足的微分方程；
答案
参考答案：由反函数求导法则，
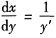，则
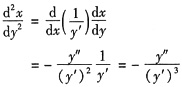，将以上两式代入所给微分方程得y"-y=sinx．
搜题请搜索小程序“爱下问搜题”
设函数y=y(x)在(-∞，+∞)内具有二阶导数，且y’≠0，x=x(y)是y=y(x)的反函数．
试将x=x(y)所满足的微分方程[*]变换为y=y(x)满足的微分方程；
参考答案：由反函数求导法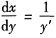则，
，则
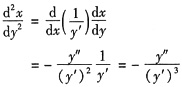，将以上两式代入所给微分方程得y"-y=sinx．