问题
填空题
设连续函数f(x)满足
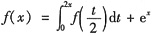 ,则f(x)=______.
,则f(x)=______.
答案
参考答案:f(x)=2e2x-ex
解析: 由
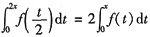 ,则
,则
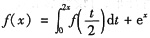 可化为f(x)=
可化为f(x)=
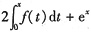 ,两边求导数得f’(x)-2f(x)=ex,解此一阶微分方程得
,两边求导数得f’(x)-2f(x)=ex,解此一阶微分方程得
f(x)=[∫ex·e∫-2dxdx+C]e-∫-2dx=(-e-x+C)e2x=Ce2x-ex
因为f(0)=1,所以有f(0)=C-1=1,即C=2,于是f(x)=2e2x-ex.
设连续函数f(x)满足
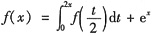 ,则f(x)=______.
,则f(x)=______.
参考答案:f(x)=2e2x-ex
解析: 由
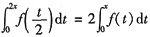 ,则
,则
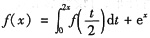 可化为f(x)=
可化为f(x)=
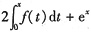 ,两边求导数得f’(x)-2f(x)=ex,解此一阶微分方程得
,两边求导数得f’(x)-2f(x)=ex,解此一阶微分方程得
f(x)=[∫ex·e∫-2dxdx+C]e-∫-2dx=(-e-x+C)e2x=Ce2x-ex
因为f(0)=1,所以有f(0)=C-1=1,即C=2,于是f(x)=2e2x-ex.