问题
单项选择题
如果y=cos2x是微分方程y’+P(x)y=0的一个特解,则该方程满足初始条件y(0)=2的特解为______
A.y=cos2x+2.
B.y=cos2x+1.
C.y=2cosx.
D.y=2cos2x.
答案
参考答案:D
解析: 因为y=cos2x是微分方程y’+P(x)y=0的一个特解.将其代入微分方程,得
-2sin2x+P(x)cos2x=0,
所以得P(x)=2tan2x.
则原微分方程为y’+2tan2x·y=0,
这是一个变量可分离的微分方程,分离变量得
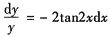 ,
,
等式两边积分,得
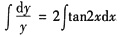 .
.
即ln|y|=ln|cos2x|+ln|C|.
于是得y=Ccos2x.由y(0)=2,得C=2.故所求特解为y=2cos2x.
