问题
填空题
微分方程y’+ytanx=cosx的通解为y=______.
答案
参考答案:(x+C)cosx,C为任意常数
解析: 此一阶线性微分方程的p(x)=tanx,q(x)=cosx,则由通解公式
y=e-∫p(x)dx[∫q(x)e∫p(x)dxx+C]
=e-∫tanxdx[∫cosxe∫tanxdxdx+C]
=
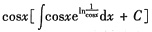
=(x+C)cosx,C为任意常数.
微分方程y’+ytanx=cosx的通解为y=______.
参考答案:(x+C)cosx,C为任意常数
解析: 此一阶线性微分方程的p(x)=tanx,q(x)=cosx,则由通解公式
y=e-∫p(x)dx[∫q(x)e∫p(x)dxx+C]
=e-∫tanxdx[∫cosxe∫tanxdxdx+C]
=
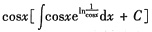
=(x+C)cosx,C为任意常数.