问题
单项选择题
设y=y(x)是二阶常系数微分方程y"+py’+qy=e3x满足初始条件y(0)=y’(0)=0的特解,则当x→0时,函数
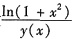 的极限______
的极限______
A.不存在.
B.等于1.
C.等于2.
D.等于3.
答案
参考答案:C
解析: 因y(0)=y’(0)=0,ln(1+0)=0,故利用洛必达法则,
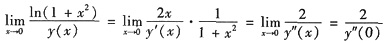 .
.
由y"+py’+qy=e3x知y"(x)连续且)y"(0)=e0=1,故所求极限等于2.
设y=y(x)是二阶常系数微分方程y"+py’+qy=e3x满足初始条件y(0)=y’(0)=0的特解,则当x→0时,函数
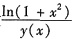 的极限______
的极限______
A.不存在.
B.等于1.
C.等于2.
D.等于3.
参考答案:C
解析: 因y(0)=y’(0)=0,ln(1+0)=0,故利用洛必达法则,
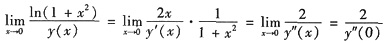 .
.
由y"+py’+qy=e3x知y"(x)连续且)y"(0)=e0=1,故所求极限等于2.