（A类）已知函数g（x）=（a+1）x-2+1（a＞0）的图象恒过定点A，且点A

问题解答题

（A类）已知函数g（x）=（a+1）^x-2+1（a＞0）的图象恒过定点A，且点A又在函数f（x）=log

（x+a）的图象上．
（1）求实数a的值；（2）解不等式f（x）＜log

a；
（3）|g（x+2）-2|=2b有两个不等实根时，求b的取值范围．
（B类）设f（x）是定义在R上的函数，对任意x，y∈R，恒有f（x+y）=f（x）+f（y）
（1）求f（0）的值；（2）求证：f（x）为奇函数；
（3）若函数f（x）是R上的增函数，已知f（1）=1，且f（2a）＞f（a-1）+2，求a的取值范围．

答案

A类：（1）∵函数g（x）=（a+1）^x-2+1（a＞0）的图象恒过定点A

∴A点的坐标为（2，2）

又因为A点在f（x）=log

（x+a）的图象上，

∴2=log

（2+a）

即a+2=3

∴a=1

（2）∵不等式f（x）＜log

a⇔log

（x+1）＜log

1=0

⇔0＜x+1＜1

⇔-1＜x＜0

∴不等式f（x）＜log

a的解集为（-1，0）

（3）∵g（x）=2^x-2+1

∴g（x+2）=2^x+1

∴|g（x+2）-2|=2b⇔|2^x+1-2|=2b⇔|2^x-1|=2b

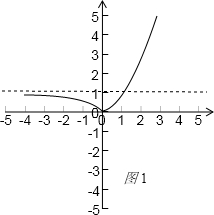
函数y=|2^x-1|的图象如图1，

要使|g（x+2）-2|=2b有两个不等实根

由图象可知需0＜2b＜1，

故b的取值范围为（0，

）

B类：（1）令x=y=0

则f（0）=f（0）+f（0）

∴f（0）=0

（2）令y=-x

则f（0）=f（x）+f（-x）

∴f（-x）=-f（x）

所以f（x）为R上的奇函数

（3）令x=y=1

则f（1+1）=f（2）=f（1）+f（1）=2

∴f（2）=2

∴f（2a）＞f（a-1）+2⇔f（2a）＞f（a-1）+f（2）⇔f（2a）＞f（a+1）

又∵f（x）是R上的增函数，所以2a＞a+1

即a＞1

∴a的取值范围为（1，+∞）