问题
问答题
设某种商品一周的需求量X是一随机变量,其概率密度为
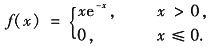
假设各周对该商品的需求量是相互独立的,
以Z表示前3周中各周需求量的最大值,求Z的概率密度fZ(z).
答案
参考答案:Z=max(X1,X2,X3),对任意实数z,有
FZ(z)=P(Z≤z)=P(max(X1,X2,X3)≤z)
=P(X1≤z,X2≤z,X3≤z)
=P(X1≤z)P(X2≤z)P(X3≤z)=[FX(z)]3.
当z≤0时,FX(z)=0.
当z>0时,
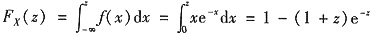 ,
,
即
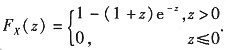 从而
从而
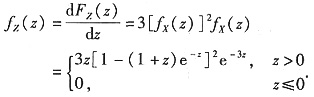
解析:[考点] 求独立随机变量函数的概率密度
