问题
问答题
已知产品某项指标X的概率密度为
其中μ为未知参数，现从产品中随机抽取3个，测得该指标为1026，966，1011.
求μ的最大似然估计值.
答案
参考答案：基于x1=1026，x2=966，x3=1011的似然函数为
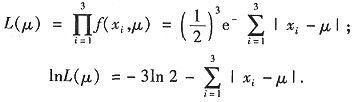
欲求lnL(μ)的最大值点，即求
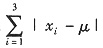的最小值点.
记
，
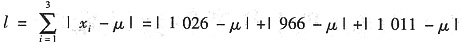当μ≤966时，l=(1026-μ)+(966-μ)+|1011-μ|
=3(1001-μ)≥3(1001-966)=105.
当μ≥1026时，l=(μ-1026)+(μ-966)+(μ-1011)
=3(μ-1001)≥3(1026-1001)=75.
当966＜μ＜1026时，l=(1026-μ)+(μ-966)+(1011-μ)
=60+|1011-μ|≥60.
(等号在μ=1011时成立).
即μ=1011时，l取最小值，lnL(μ)取最大值. 从而
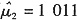是μ的最大似然估计值.
解析：[考点] 求矩估计值和最大似然估计值