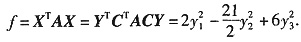问题
问答题
已知矩阵
 与对角矩阵相似.
与对角矩阵相似.
求坐标变换X=CY,化二次型f=XTAX为标准形.
答案
参考答案:
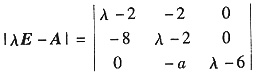
=(λ-6)(λ2-4λ-12)=(λ-6)2(λ+2)=0,
得A的特征值为λ1=λ2=6,λ3=-2.
由A与对角矩阵相似知A属于λ1=λ2=6的有两个线性无关的特征向量.
即(6E-A)X=0的基础解系有2个解向量:3-r(6E-A)=2,故r(6E-A)=1.
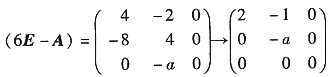 .得a=0.
.得a=0.
此时二次型为

令
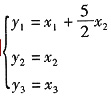 ,即
,即
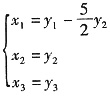 ,亦即
,亦即
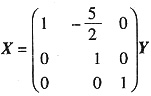 ,则有
,则有