问题
问答题
设平面图形A由x2+y2≤2x与y≥x围成，求图形A绕直线x=2旋转一周所得旋转体的体积.
答案
参考答案：以y为积分变量，则A的边界曲线为
x2=y(0≤y≤1).
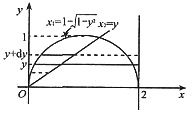
所求体积为曲线x1=x1(y)和x2=x2(y)绕直线x=2所得旋转体体积之差，
取y，y+dy∈[0，1]，由微元法知
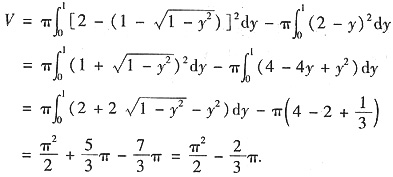
解析：[考点] 定积分应用
搜题请搜索小程序“爱下问搜题”
设平面图形A由x2+y2≤2x与y≥x围成，求图形A绕直线x=2旋转一周所得旋转体的体积.
参考答案：以y为积分变量，则A的边界曲线为
x2=y(0≤y≤1).
所求体积为曲线x1=x1(y)和x2=x2(y)绕直线x=2所得旋转体体积之差，
取y，y+dy∈[0，1]，由微元法知
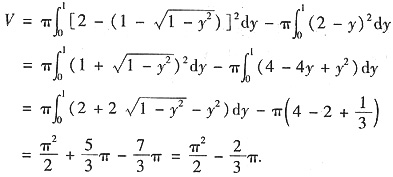
解析：[考点] 定积分应用