问题
问答题
设A为n阶矩阵,r(A)=n-1,且代数余子式A11≠0.
求AX=0的通解;
答案
参考答案:由于r(A)=n-1<n,故AX=0必有非零解X=(x1,x2,…,xn)T≠0. 且它的基础解系含有n-r(A)=n-(n-1)=1个解向量. 将此非零解代入AX=0,有
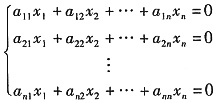
当考查n-1元方程组:

时,由于其系数行列式A11≠0,根据克莱姆法则,它只有零解x2=x3=…=xn=0,从而知x1≠0(否则X=(x1,x2…xn)T=0与其AX=0非零解矛盾). 故AX=0的基础解系为ξ=(1,0,0,…,0)T,AX=0的通解为X=cξ(c为任意常数).
