不等式x²-log_mx＜0在（0，

2

2

）内恒成立，

转化为不等式x²＜log_mx在（0，

2

2

）内恒成立，

即x∈（0，

2

2

）时，函数f（x）=x²的图象恒在g（x）=log_mx的图象的下方．

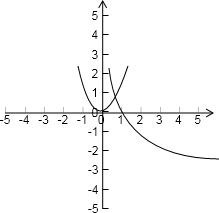
由图象可知0＜m＜1，若x=

2

2

时两图象相交，

即(

2

2

)2=logm

2

2

，解得m=

1

2

，

所以结合图象可得实数m的取值范围是

1

2

≤m＜1．

故选D．