问题
问答题
设u=u(x，y)在全平面上有连续偏导数，
(Ⅰ) 作极坐标变换x=rcosθ，y=rsinθ，求
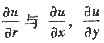的关系式；
(Ⅱ) 若
(
(x，y))，求证：u(x，y)为常数；
(Ⅲ) 若
(x2+y2≥R2＞0)，求证：
．
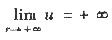答案
参考答案：(Ⅰ) 由复合函数求导法[*]
[*]
(Ⅱ) 由题(Ⅰ)，[*]
又u(rcosθ，rsinθ)对r在[0，+∞)上连续[*]
u(x，y)=u(rcosθ，rsinθ)=u(rcosθ，rsinθ)|r=0=u(0，0)([*](x，y))．
(Ⅲ) 由题(Ⅰ)，有[*]．对r从R到r积分得
[*]
注意，u(Rcosθ，Rsinθ)对θ∈[0，2π]上连续，故有界。
又由[*]
因此[*]