问题
问答题
设f(x)满足
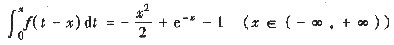 ,
,
(Ⅰ) 讨论f(x)在(-∞,+∞)是否存在最大值或最小值,若存在则求出;
(Ⅱ) 求y=f(x)的渐近线方程.
答案
参考答案:(Ⅰ) 先求出f(x)的表达式.
由[*],
得[*]
上式中令x=0,等式显然成立.又两边求导得
f(-x)=-x-e-x.
因此,f(x)=x-ex,x∈(-∞,+∞).
下面讨论f(x)的最值问题.由
[*]
f(0)=-1是f(x)在(-∞,+∞)的最大值.f(x)在(-∞,+∞)无最小值.
(Ⅱ) [*]
x→-∞时有渐近线y=x.又f(x)无间断点,且
[*]
[*]y=f(x)无其他渐近线.
