问题
问答题
已知an是以a为首项,q为公比的等比数列,Sn为它的前n项和.
(1)当S1、53、S4成等差数列时,求q的值;
(2)当Sm、Sn、Sl成等差数列时,求证:对任意自然数k,am+k、an+k、al+k也成等差数列,
答案
参考答案:
(1)由已知,an=aqn-1,
因此S1=a,S3=a(1+q+q2),S4=a(1+q+q2+q3).
当S1、S3、S4成等差数列时,S1+S4=2S3,可得aq3=aq+aq2.
化简得q2-q-1=0,解得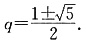
(2)若q=1,则{an}的每项an-a,此时am+k、an+k、al+k显然成等差数列,
若q≠1,由Sm、Sn、Sl成等差数列可得Sm+Sl-2Sn,即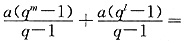
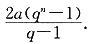
整理得qm+ql=2qn,因此,am+k+al+k=aqk-1(qm+ql)=2aqn+k-1=2an+k.
所以,am+k、an+k、al+k也成等差数列.
