问题
问答题
设两随机变量(X，Y)在区域D上为均匀分布，其中D=(x，y):|x|+|y|1≤1，又设U=X+Y，V=X-Y，试求：
(Ⅰ)U与V的概率密度fu(u)与fv(v)；
(Ⅱ)U与V的协方差cov(U，V)的相关系数ρUV。
答案
参考答案：区域D是以(-1，0)，(1，0)，(0，1)，(0，-1)为顶点的正方形区域，D的面积为2，
(X，Y)的联合密度为f(x，y)=
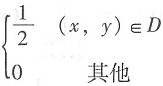，此可以利用f(x，y)的对称性，求fU(u)和fV(v)。
(Ⅰ)U=X+Y，FU(u)=P{U≤u}=P{X+Y≤u}=
。
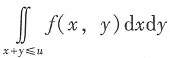当u＜-1时，FU(u)=0；
当-1≤u≤1时，FU(u)=
；
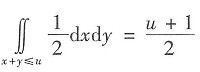当u＞1时，FU(u)=1，
，
V=X-Y，FV(v)=P{V≤v}=P{X-Y≤u}=
。
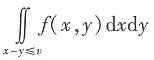当v＜-1时，FV(v)=0；
当-1≤v≤1时，
；
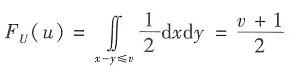当v＞1时，FV(v)=1，
。
(Ⅱ)cov(U，V)=E(UV)-EU·EV，显然EU=EV=0，
而E(UV)=E((X+Y)(X-Y))=E(X2-Y2)=EX2-EY2，
由于X，Y的对称性得EX2=EY2，所以cov(U，V)=0，
。
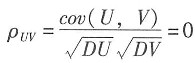解析：[考点] 随机变量的概率密度及相关系数