问题
问答题
设生产某种产品需投入甲、乙两种原料，x和y分别为甲、乙两种原料的投入量(单位：吨)，Q为产出量，且生产函数为Q=kxαyβ，其中常数k＞0，α＞0，β＞0。已知甲种原料每吨的价格为P1(单位：万元)，乙种原料每吨的价格为P2(单位：万吨)。如果投入总价值为A(万元)的这两种原料，当每种原料各投入多少吨时，才能获得最大的产出量
答案
参考答案：本题要求函数Q=kxαyβ在条件P1x+P2y-A=0下的最大值点，用拉格朗日系数法，构造拉格朗日函数F(x，y，λ)=kxαyβ+λ(P1x+P2y-A)，
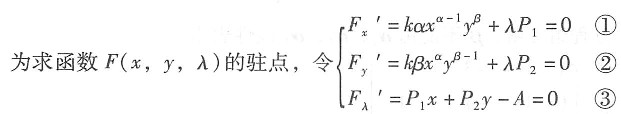
由①、②消去参数λ
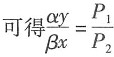，即
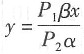，代入③不难计算出唯一驻点
，
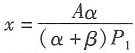，因驻点唯一，且实际问题必存在最大产量，所以计算结果表明，当投入总价值为A(万元)的甲、乙两种原料时，使产量Q最大的甲、乙两种原料的投入量分别是
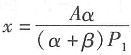(吨)与
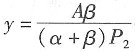(吨)。
解析：[考点] 微积分在经济中的应用
四种元素中，最高正化合价数值最大的是P
（硅烷）比
稳定