参考答案：

[分析]： 本题是要证明存在两个不同的点ξ，η∈(0，1)，使得

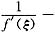
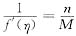，这里不能在同一区间(0，1)上用两次中值定理，因为无法说明ξ≠η．因此，往往需要将区间[0，1]分为两个区间[0，c]和[c，1](其中0＜c＜1)．然后，分别在区间[0，c]和[c，1]上用拉格朗日中值定理，这里的关键和难点是c点的选取．一种有效的方法是c点待定，先在[0，c]和[c，1]上分别用拉格朗日中值定理，将f′(ξ)和f′(η)代入要证的结论

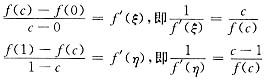中来确定c．
由拉格朗日中值定理知，存在ξ∈(0，c)，η∈(c，1)使

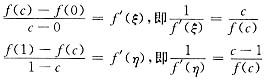
要使

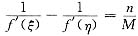
即

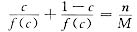
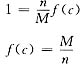
若能证明至少存在一点c∈(0，1)，使

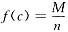，分点c就应选使

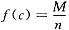的点．
[证] 由于f(x)在[0，1]上连续，则f(x)在[0，1]上有最大值M和最小值m，由题设知M＞0，由于f(0)=f(1)=0，则m≤0，从而有

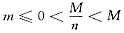
由连续函数的介值定理知，至少存在一点c∈(0，1)，使

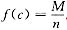．由拉格朗日中值定理知存在ξ∈(0，c)，η∈(c，1)，使

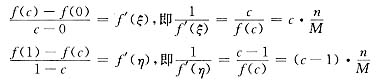
则

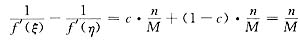
[评注] 本题的方法代表了微分中值定理证明题中一类问题的解决方法．题目的特点是证明存在两个不同的点ξ，η∈(a，b)，使得关于f′(ξ)和f′(η)某个等式成立．