问题
问答题
已知曲线y=f(x)和
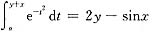 在原点处相切,试求极限
在原点处相切,试求极限
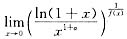 .
.
答案
参考答案:
[分析]: 首先利用曲线y=f(x)和
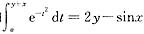 在原点处相切,可求得a和f′(0),然后再进一步求极限
在原点处相切,可求得a和f′(0),然后再进一步求极限
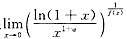 .
.
[解] 由于曲线y=f(x)和
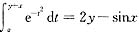 在原点处相切,则f(0)=0,
在原点处相切,则f(0)=0,
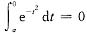
从而有a=0
等式
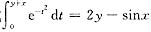 两端对x求导得
两端对x求导得
e-(y+x)2(y′+1)=2y′-cosx
将x=0,y=0代入上式得y′(0)=2
则f′(0)=2
 .
.
这是一个“1∞”型极限,而
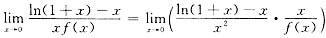
而
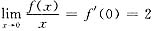 .
.
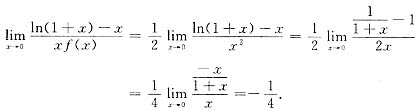
则
 ,
,
故
 .
.
[评注] 本题主要考查导数的定义及几何意义,变上限求导,“1∞”型极限,是一道综合性较强的题目.
