问题
问答题
设抛物线y=ax2+bx+c通过点(0，0)和(1，2)，且a＜0，试确定a，b，c的值使该抛物线与x轴所围图形D的面积最小，并求此图形D绕直线x=2旋转一周所得旋转体的体积．
答案
参考答案：[解] 由抛物线y=ax2+bx+c过点(0，0)和(1，2)知
c=0，a+b=2．
又a＜0，则b＞2．
令ax2+bx=0，得x1=0，
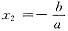
则图形D的面积为
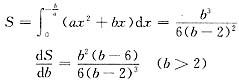
令
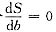，得b=6
且当2＜b＜6时，
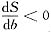，当b＞6时，
，
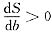则当b=6时，S取得最小值，此时，a=-4，抛物线方程为
y=-4x2+6x
为求D绕x=2旋转所得旋转体体积，先建立体积微元
dV=2π(2-x)ydx=2π(2-x)(6x-4x2)dx
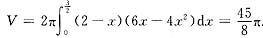
[评注] 本题主要考察平面域的面积和旋转体的体积．