问题
单项选择题
已知f(x，y)在(0，0)点连续，且
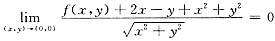
则下列结论不正确的是
(A) f(x，y)在(0，0)点可微．
(B) fx(0，0)=-2．
(C) fy(0，0)=1．
(D) fx(0，0)和fy(0，0)都不一定存在．
答案
参考答案：D
解析：
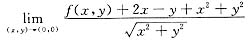
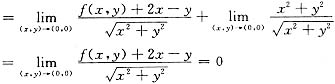
由于上式分母趋于零，则其分子趋于零，由f(x，y)的连续性知f(0，0)=0从而有
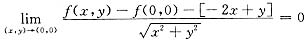
即f(x，y)-f(0，0)=-2x+y+0(ρ)
其中
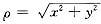，由微分的定义知，f(x，y)在(0，0)点可微，且f′x(0，0)=-2，f′y(0，0)=1，故(D)不正确．