某一非确定性有限自动机(NFA)的状态转换图如图6-1所示,该NFA等价的正规式是 (1) ,与该NFA等价的DFA是 (2) 。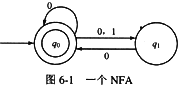
2()
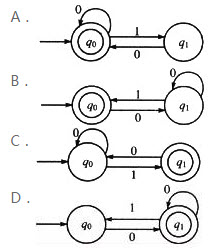
A.A
B.B
C.C
D.D
参考答案:A
解析:
我们先介绍有关概念和规则。
1.有限状态自动机
一个确定的有限状态自动机M(记做DFA)是一个五元组:
M=(∑,Q,q0,F,δ)
其中:
(1)Q是一个有限状态集合;
(2)∑是一个字母表,其中的每个元素称为一个输入符号;
(3)q0∈Q,称为初始状态;
(4)F[*]Q,称为终结状态集合;
(5)δ是一个从Q×∑(Q与∑的笛卡儿乘积)到Q的单值映射:
δ(q,a)=q’ (q,q’∈Q, a∈∑)
表示当前状态为q,输入符号为a时,自动机将转换到下一个状态q’,q’称为q的一个后继。
若Q={q1,q2,…,qn),∑={a1,a2,…,an),则(δ(qi,aj))n×m是一个n行m列矩阵,称为DFA的状态转换矩阵,或称转换表。
有限状态自动机可以形象地用状态转换图表示,设有限状态自动机:
DFA M=({S,A,B,C,f},{1,0},S,{f},δ),
其中:
δ(S,0)=B,δ(S,1)=A,δ(A,0)=f,δ(A,1)=C,δ(B,0)=C,δ(B,1)=f,
δ(C,0)=f,δ(C,1)=f
其对应的状态转换图如图6-2所示。
[*]
图6-2中的圈表示状态结点,其中双圈表示终结状态结点。而边表示状态的转换,代表映射。边上的符号表示此转换需要输入的符号,代表映射的输入。
对于∑上的任何字符串w∈∑*,若存在一条从初态结点到终态结点的路径,在这条路径上的所有边的符号连接成的符号串恰好是w,则w被DFA所识别(或接受、读出)。 DFA所能识别的符号串的全体记为L(M),称为DFA所识别的语言。如果对所有W∈∑*,以下述的递归方式扩张δ的定义:
δ(q,ε)=q
δ(q,wa)=δ(δ(q,w),a),对任何a∈∑,q∈Q
我们则可以把DFA所识别的语言形式定义为:
L(M)={w|w∈∑*,若存在q∈F,使δ(q0,w)=q
前面介绍的是确定的有限自动机,即一个状态对于特定的输入字符有一个确定的后继状态。而当一个状态对于特定的输入字符有一个以上的后继状态时,我们称该有限自动机为非确定有限自动机(记做NFA),其形式定义如下。
一个非确定的有限自动机M是一个五元组:
M=(∑,Q,q0,F,δ)
其中∑,Q,q0,F的意义和DFA的定义一样,而δ一个从Q×∑到Q的子集的映射,即δ:Q×∑→2Q,其中2Q是Q的幂集,即Q的所有子集组成的集合。
与DFA一样,NFA同样可以用状态转换图表示,所不同的是,在图中一个状态结点可能有一条以上的边到达其他状态结点。同样,对于任何字符串W∈∑*,若存在一条从初态结点到终态结点的路径,在这条路径上的所有边的符号连接成的符号串恰好是 w,则称w为NFA所识别(或接受或读出)。若q0正几这时q0既是初始状态,也是终结状态,因而有一条从初态结点到终态结点的ε-路径,此时空符号串可以被NFA接受。 NFA所能识别的符号串的全体记为L(M),称为NFA所识别的语言。
对任何一个NFA,都存在一个DFA’使L(M’)=L(M),这时我们称M’与M等价。构造与M等价的M’的基本方法是让M’的状态对应于M的状态集合。即如果有δ(q,a)={q1,q2,…,qn),则把{q1,q2,…,qn)看做M’的一个状态,即M’中的状态集合Q’的一个元素。
对于一个NFA,如果我们把δ扩展为从Q×∑U{ε}到2Q的映射,则我们称该自动机为带ε-转移的非确定有限自动机。同样,对于带ε-转移的非确定有限自动机,我们也可以构造与之等价的不带ε-转移的非确定有限自动机。
2.正规表达式
正规表达式(正规式)是一个十分有用的概念,它紧凑地表达有限自动机所接受的语言。对正规表达式的递归定义为:一个正规表达式是按照一组定义规则由一些较简单的正规表达式所组成的。在字母表∑上的正规表达式可以使用以下规则定义:
(1)ε和Φ是∑上的正规表达式,它们所表示的语言分别为{ε}和Φ。
(2)如果a是∑内的一个符号,则a是一个正规表达式,所表示的语言为{a},即包含符号串a的集合。
(3)如果r和s分别是表示语言L(r)和L(s)的正规表达式,那么:
(r)|(s)是一个表示L(r)∪L(s)的正规表达式。
(r)(s)是一个表示L(r)L(s)的正规表达式。
(r)*是一个表示(L(r))*的正规表达式。
(r)是一个表示L(r)的正规表达式。
通常在正规表达式中,一元运算符“*”具有最高的优先级,连接运算具有次优先级,运算符“|”具有最低优先级,这三个运算都是左结合的。每一个正规表达式只都对应一个有限自动机M,使M所接受的语言就是正规表达式的值。经过以下步骤可以从一个正规表达式R构造出相应的有限自动机M。
首先定义初始状态S和终止状态f并且组成有向图,如图6-3所示。
[*]
然后反复应用以下规则:
[*]
直到所有的边都以∑中的字母或ε标记为止。由此产生了一个带ε-转移的非确定有限自动机,然后可以通过上面介绍的方法,把该自动机转换成确定有限状态自动机。
3.试题解答
从图6-1可以看出,从q0状态出发,可以只输入若干个0,仍然回到q0状态;也可以只输入若干个0,经由q1状态后再回到q0状态;还可以输入1后,到达q1,然后再输入0,回到q0状态。因此,得出其正规式为(0|((0|1)0))T根据正规式之间的代数性质得0*((0|1)0)*
根据图6-1的NFA,下面求与之等价的DFA。
T0=ε-closure{q0}={q0},T0未被标记,为子集中唯一成员;
令T1=ε-closure{move(T0,0)}={q0,q1},将T1加入子集;
令T2=ε-closure{move(T0,1)}={q1},将T2加入子集:
ε-closure{move(T1,0)}={q0,q1),即T1,已经在子集中;
ε-closure{move(T1,1)}={q1),即T2,已经在子集中;
ε-closure{move(T2,0)}={q0},即T0,已经在子集中。
因此,构造了三个子集T0={q0}、T1={q0,q1}、T2={q1},如图6-4所示。
[*]
首先,将图6-4中状态分为终态和非终态两个子集即({T0,T1),{T2}),再进行子集划分,观察第一个子集{T0,T1},输入0和1后成为的状态一样。因此,{T0,T1)两个状态可以合并成为一个状态,变换即得选项A的状态。
