问题
问答题
设
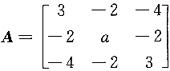，若方程组(2E+A)x=0存在非零解，求a的值，并求正交矩阵Q，使QTA2Q为对角矩阵．
答案
参考答案：由
．
，
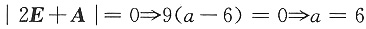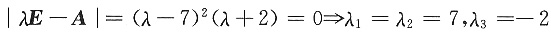解得特征向量：α1=(1，-2，0)T，α2=(1，0，-1)T，α3=(2，1，2)T，
将α1，α2正交化：
再单位化β1，β2，α3：
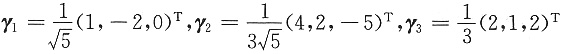
令 Q=[γ1，γ2，γ3]，
则
．
搜题请搜索小程序“爱下问搜题”
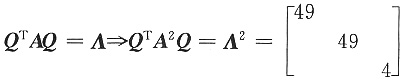设
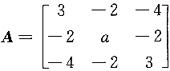，若方程组(2E+A)x=0存在非零解，求a的值，并求正交矩阵Q，使QTA2Q为对角矩阵．
参考答案：由
．
，
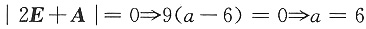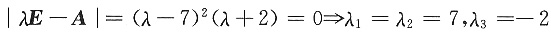解得特征向量：α1=(1，-2，0)T，α2=(1，0，-1)T，α3=(2，1，2)T，
将α1，α2正交化：
再单位化β1，β2，α3：
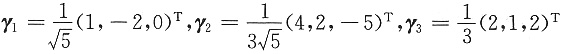
令 Q=[γ1，γ2，γ3]，
则
．
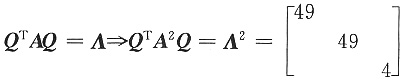